Bootstrap Examples¶
This setup code is required to run in an IPython notebook
[1]:
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn
seaborn.set_style("darkgrid")
plt.rc("figure", figsize=(16, 6))
plt.rc("savefig", dpi=90)
plt.rc("font", family="sans-serif")
plt.rc("font", size=14)
Sharpe Ratio¶
The Sharpe Ratio is an important measure of return per unit of risk. The example shows how to estimate the variance of the Sharpe Ratio and how to construct confidence intervals for the Sharpe Ratio using a long series of U.S. equity data.
[2]:
import arch.data.frenchdata
import numpy as np
import pandas as pd
ff = arch.data.frenchdata.load()
The data set contains the Fama-French factors, including the excess market return.
[3]:
excess_market = ff.iloc[:, 0]
print(ff.describe())
Mkt-RF SMB HML RF
count 1109.000000 1109.000000 1109.000000 1109.000000
mean 0.659946 0.206555 0.368864 0.274220
std 5.327524 3.191132 3.482352 0.253377
min -29.130000 -16.870000 -13.280000 -0.060000
25% -1.970000 -1.560000 -1.320000 0.030000
50% 1.020000 0.070000 0.140000 0.230000
75% 3.610000 1.730000 1.740000 0.430000
max 38.850000 36.700000 35.460000 1.350000
The next step is to construct a function that computes the Sharpe Ratio. This function also return the annualized mean and annualized standard deviation which will allow the covariance matrix of these parameters to be estimated using the bootstrap.
[4]:
def sharpe_ratio(x):
mu, sigma = 12 * x.mean(), np.sqrt(12 * x.var())
values = np.array([mu, sigma, mu / sigma]).squeeze()
index = ["mu", "sigma", "SR"]
return pd.Series(values, index=index)
The function can be called directly on the data to show full sample estimates.
[5]:
params = sharpe_ratio(excess_market)
params
[5]:
mu 7.919351
sigma 18.455084
SR 0.429115
dtype: float64
Reproducibility¶
All bootstraps accept the keyword argument seed which can contain a NumPy Generator or RandomState or an int. When using an int, the argument is passed np.random.default_rng to create the core generator. This allows the same pseudo random values to be used across multiple runs.
Warning¶
The bootstrap chosen must be appropriate for the data. Squared returns are serially correlated, and so a time-series bootstrap is required.
Bootstraps are initialized with any bootstrap specific parameters and the data to be used in the bootstrap. Here the 12 is the average window length in the Stationary Bootstrap, and the next input is the data to be bootstrapped.
[6]:
from arch.bootstrap import StationaryBootstrap
# Initialize with entropy from random.org
entropy = [877788388, 418255226, 989657335, 69307515]
seed = np.random.default_rng(entropy)
bs = StationaryBootstrap(12, excess_market, seed=seed)
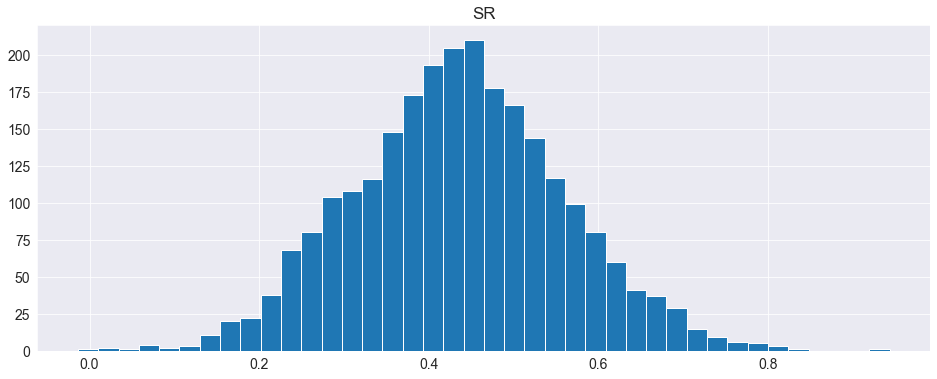
results = bs.apply(sharpe_ratio, 2500)
SR = pd.DataFrame(results[:, -1:], columns=["SR"])
fig = SR.hist(bins=40)
[7]:
cov = bs.cov(sharpe_ratio, 1000)
cov = pd.DataFrame(cov, index=params.index, columns=params.index)
print(cov)
se = pd.Series(np.sqrt(np.diag(cov)), index=params.index)
se.name = "Std Errors"
print("\n")
print(se)
mu sigma SR
mu 3.837196 -0.638431 0.224722
sigma -0.638431 3.019569 -0.105762
SR 0.224722 -0.105762 0.014915
mu 1.958876
sigma 1.737691
SR 0.122126
Name: Std Errors, dtype: float64
[8]:
ci = bs.conf_int(sharpe_ratio, 1000, method="basic")
ci = pd.DataFrame(ci, index=["Lower", "Upper"], columns=params.index)
print(ci)
mu sigma SR
Lower 4.367662 14.780547 0.166759
Upper 11.958503 21.735752 0.659350
Alternative confidence intervals can be computed using a variety of methods. Setting reuse=True allows the previous bootstrap results to be used when constructing confidence intervals using alternative methods.
[9]:
ci = bs.conf_int(sharpe_ratio, 1000, method="percentile", reuse=True)
ci = pd.DataFrame(ci, index=["Lower", "Upper"], columns=params.index)
print(ci)
mu sigma SR
Lower 3.880198 15.174416 0.198880
Upper 11.471040 22.129620 0.691471
Optimal Block Length Estimation¶
The function optimal_block_length can be used to estimate the optimal block lengths for the Stationary and Circular bootstraps. Here we use the squared market return since the Sharpe ratio depends on the mean and the variance, and the autocorrelation in the squares is stronger than in the returns.
[10]:
from arch.bootstrap import optimal_block_length
opt = optimal_block_length(excess_market**2)
print(opt)
stationary circular
Mkt-RF 47.766787 54.679322
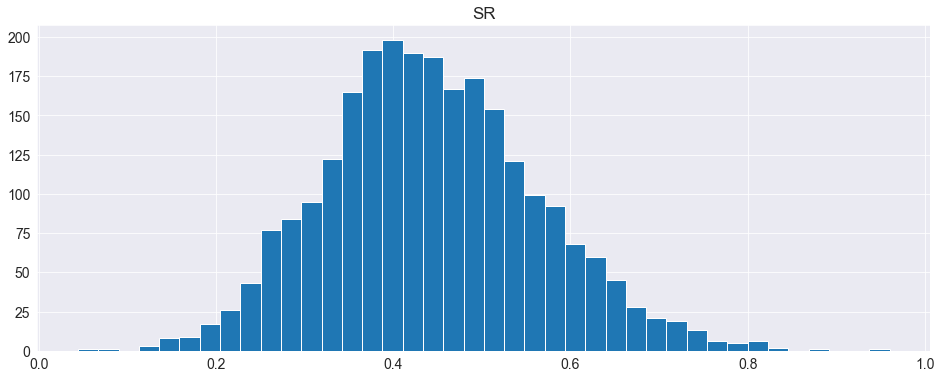
We can repeat the analysis above using the estimated optimal block length. Here we see that the extremes appear to be slightly more extreme.
[11]:
# Reinitialize using the same entropy
rs = np.random.default_rng(entropy)
bs = StationaryBootstrap(opt.loc["Mkt-RF", "stationary"], excess_market, seed=seed)
results = bs.apply(sharpe_ratio, 2500)
SR = pd.DataFrame(results[:, -1:], columns=["SR"])
fig = SR.hist(bins=40)
Probit (statsmodels)¶
The second example makes use of a Probit model from statsmodels. The demo data is university admissions data which contains a binary variable for being admitted, GRE score, GPA score and quartile rank. This data is downloaded from the internet and imported using pandas.
[12]:
import arch.data.binary
binary = arch.data.binary.load()
binary = binary.dropna()
print(binary.describe())
admit gre gpa rank
count 400.000000 400.000000 400.000000 400.00000
mean 0.317500 587.700000 3.389900 2.48500
std 0.466087 115.516536 0.380567 0.94446
min 0.000000 220.000000 2.260000 1.00000
25% 0.000000 520.000000 3.130000 2.00000
50% 0.000000 580.000000 3.395000 2.00000
75% 1.000000 660.000000 3.670000 3.00000
max 1.000000 800.000000 4.000000 4.00000
Fitting the model directly¶
The first steps are to build the regressor and the dependent variable arrays. Then, using these arrays, the model can be estimated by calling fit
[13]:
import statsmodels.api as sm
endog = binary[["admit"]]
exog = binary[["gre", "gpa"]]
const = pd.Series(np.ones(exog.shape[0]), index=endog.index)
const.name = "Const"
exog = pd.DataFrame([const, exog.gre, exog.gpa]).T
# Estimate the model
mod = sm.Probit(endog, exog)
fit = mod.fit(disp=0)
params = fit.params
print(params)
Const -3.003536
gre 0.001643
gpa 0.454575
dtype: float64
The wrapper function¶
Most models in statsmodels are implemented as classes, require an explicit call to fit and return a class containing parameter estimates and other quantities. These classes cannot be directly used with the bootstrap methods. However, a simple wrapper can be written that takes the data as the only inputs and returns parameters estimated using a Statsmodel model.
[14]:
def probit_wrap(endog, exog):
return sm.Probit(endog, exog).fit(disp=0).params
A call to this function should return the same parameter values.
[15]:
probit_wrap(endog, exog)
[15]:
Const -3.003536
gre 0.001643
gpa 0.454575
dtype: float64
The wrapper can be directly used to estimate the parameter covariance or to construct confidence intervals.
[16]:
from arch.bootstrap import IIDBootstrap
bs = IIDBootstrap(endog=endog, exog=exog)
cov = bs.cov(probit_wrap, 1000)
cov = pd.DataFrame(cov, index=exog.columns, columns=exog.columns)
print(cov)
Const gre gpa
Const 0.397473 -6.641971e-05 -0.102525
gre -0.000066 4.467596e-07 -0.000058
gpa -0.102525 -5.815162e-05 0.039859
[17]:
se = pd.Series(np.sqrt(np.diag(cov)), index=exog.columns)
print(se)
print("T-stats")
print(params / se)
Const 0.630455
gre 0.000668
gpa 0.199647
dtype: float64
T-stats
Const -4.764077
gre 2.457413
gpa 2.276894
dtype: float64
[18]:
ci = bs.conf_int(probit_wrap, 1000, method="basic")
ci = pd.DataFrame(ci, index=["Lower", "Upper"], columns=exog.columns)
print(ci)
Const gre gpa
Lower -4.214157 0.000360 0.005706
Upper -1.622607 0.002906 0.871725
Speeding things up¶
Starting values can be provided to fit which can save time finding starting values. Since the bootstrap parameter estimates should be close to the original sample estimates, the full sample estimated parameters are reasonable starting values. These can be passed using the extra_kwargs dictionary to a modified wrapper that will accept a keyword argument containing starting values.
[19]:
def probit_wrap_start_params(endog, exog, start_params=None):
return sm.Probit(endog, exog).fit(start_params=start_params, disp=0).params
[20]:
bs.reset() # Reset to original state for comparability
cov = bs.cov(
probit_wrap_start_params, 1000, extra_kwargs={"start_params": params.values}
)
cov = pd.DataFrame(cov, index=exog.columns, columns=exog.columns)
print(cov)
Const gre gpa
Const 0.397473 -6.641971e-05 -0.102525
gre -0.000066 4.467596e-07 -0.000058
gpa -0.102525 -5.815162e-05 0.039859
Bootstrapping Uneven Length Samples¶
Independent samples of uneven length are common in experiment settings, e.g., A/B testing of a website. The IIDBootstrap allows for arbitrary dependence within an observation index and so cannot be naturally applied to these data sets. The IndependentSamplesBootstrap allows datasets with variables of different lengths to be sampled by exploiting the independence of the values to separately bootstrap each component. Below is an example showing how a confidence interval can be constructed
for the difference in means of two groups.
[21]:
from arch.bootstrap import IndependentSamplesBootstrap
def mean_diff(x, y):
return x.mean() - y.mean()
rs = np.random.RandomState(0)
treatment = 0.2 + rs.standard_normal(200)
control = rs.standard_normal(800)
bs = IndependentSamplesBootstrap(treatment, control, seed=seed)
print(bs.conf_int(mean_diff, method="studentized"))
[[0.19450863]
[0.49723719]]